Tricky Puzzles - Topic 3

samuelthx · Post by **samuelthx** » Mon Jan 13, 2014 1:16 am

Aw. And I was so close too.

(actually my answer works too but whatever)
Now for the next puzzle--how would you have nine queens on the board which cannot eliminate each other? You are allowed one pawn

Sammy_P · Post by **Sammy_P** » Mon Jan 13, 2014 1:18 am

Jutomi wrote:You know, like one queen human would throw a rock at an other queen human, and she'd be unconscious.

If she's unconscious for the rest of her life, she's out of the game.

Jutomi · Post by **Jutomi** » Mon Jan 13, 2014 2:30 am

Just looking at almost all possibilities, here.
Though, I apparently didn't when I forgot to mention the paint thing.

Here's an other one for you - and it's not calculus.

76=3171, 587=8102, and 1462=115.

What would 5000 be?

Edit: Fixed the third number.
Edit: Fixed the third number again.

Jutomi · Post by **Jutomi** » Tue Jan 14, 2014 5:30 am

samuelthx wrote:Aw. And I was so close too. (actually my answer works too but whatever)
Now for the next puzzle--how would you have nine queens on the board which cannot eliminate each other? You are allowed one pawn

This is hard!

samuelthx · Post by **samuelthx** » Tue Jan 14, 2014 10:20 am

Jutomi wrote:
samuelthx wrote:Aw. And I was so close too. (actually my answer works too but whatever)
Now for the next puzzle--how would you have nine queens on the board which cannot eliminate each other? You are allowed one pawn
This is hard!

Yours too!

Or maybe I'm just bad at number puzzles.

As for my puzzle, there are multiple solutions to this. And there are no special tricks involved--just hardcore thinking.

yot yot5 · Post by **yot yot5** » Tue Jan 14, 2014 1:42 pm

samuelthx wrote:Now for the next puzzle--how would you have nine queens on the board which cannot eliminate each other? You are allowed one pawn

This is impossible, unless you use a trick. With 8 queens, there will be one queen on every row and every column. The 9th queen will also have to take up one row and one column, which means it will be able to "see" at least 2 other queens. You only have 1 pawn, so it's impossible to block off every attack route.

samuelthx · Post by **samuelthx** » Tue Jan 14, 2014 2:09 pm

yot yot5 wrote:
samuelthx wrote:Now for the next puzzle--how would you have nine queens on the board which cannot eliminate each other? You are allowed one pawn
This is impossible, unless you use a trick. With 8 queens, there will be one queen on every row and every column. The 9th queen will also have to take up one row and one column, which means it will be able to "see" at least 2 other queens. You only have 1 pawn, so it's impossible to block off every attack route.

There is absolutely no trick involved.
It is far from impossible. In fact, there are multiple ways this can be done.

Edit: Think very carefully about what the presence of the pawn really implies.

Tell me if you want a hint

samuelthx · Post by **samuelthx** » Tue Jan 14, 2014 2:24 pm

Jutomi wrote:Just looking at almost all possibilities, here.
Though, I apparently didn't when I forgot to mention the paint thing.

Here's an other one for you - and it's not calculus.

76=3171, 587=8102, and 1462=115.

What would 5000 be?

Edit: Fixed the third number.
Edit: Fixed the third number again.

Gah.
The reason why I'm so bad at number puzzles is because the pattern or relationship could be anything!
I know my solve:fail ratio is already out of whack but...
Hint please, Jutomi

Muzozavr · Post by **Muzozavr** » Tue Jan 14, 2014 4:35 pm

samuelthx wrote:
yot yot5 wrote:
samuelthx wrote:Now for the next puzzle--how would you have nine queens on the board which cannot eliminate each other? You are allowed one pawn
This is impossible, unless you use a trick. With 8 queens, there will be one queen on every row and every column. The 9th queen will also have to take up one row and one column, which means it will be able to "see" at least 2 other queens. You only have 1 pawn, so it's impossible to block off every attack route.
There is absolutely no trick involved.
It is far from impossible. In fact, there are multiple ways this can be done.
Edit: Think very carefully about what the presence of the pawn really implies.

Tell me if you want a hint

I specifically avoided google searching to solve the puzzle by myself.

So, using a website that allowed me to drag-and-drop pieces and then generate a diagram image without me having to save the screenshot manually...

It really does work!

yot yot5 · Post by **yot yot5** » Tue Jan 14, 2014 4:51 pm

Muzozavr wrote:
samuelthx wrote:
yot yot5 wrote:
samuelthx wrote:Now for the next puzzle--how would you have nine queens on the board which cannot eliminate each other? You are allowed one pawn
This is impossible, unless you use a trick. With 8 queens, there will be one queen on every row and every column. The 9th queen will also have to take up one row and one column, which means it will be able to "see" at least 2 other queens. You only have 1 pawn, so it's impossible to block off every attack route.
There is absolutely no trick involved.
It is far from impossible. In fact, there are multiple ways this can be done.
Edit: Think very carefully about what the presence of the pawn really implies.

Tell me if you want a hint
I specifically avoided google searching to solve the puzzle by myself.

So, using a website that allowed me to drag-and-drop pieces and then generate a diagram image without me having to save the screenshot manually...

It really does work!

Oh, right. I see. Place the pawn in the middle of a queen "cross".

That was an awesome puzzle, even if I got it completely wrong.

Jutomi · Post by **Jutomi** » Tue Jan 14, 2014 5:50 pm

Here's a hint for my other puzzle.

It goes ###, and involves lots of things involving circles and momentum.

If that just makes it more confusing for you, though, then just ignore the hints.

Muzozavr · Post by **Muzozavr** » Tue Jan 14, 2014 6:36 pm

Here's another chess-queen puzzle, this one is by Frangen:

Place 10 white queens and 9 black queens on an 8x8 board so that no two queens of opposite colors are attacking each other.

(which means: white can attack white, black can attack black, BUT white cannot attack black)

This one is actually pretty hard, but I did manage to solve it.

Jutomi · Post by **Jutomi** » Tue Jan 14, 2014 8:10 pm

It's so much easier figuring out how to put 16 of each on a board...

I am lost.

Muzozavr · Post by **Muzozavr** » Tue Jan 14, 2014 8:48 pm

16 of each

You mean 8 of each, right? Which would make 16 in total.

Yeah, 8 of each has a pretty obvious solution that easily transforms into a "8+9" which might confuse you... because the "10+9" solution is totally different!! Forget your obvious 8 of each scheme and work from scratch.

As a matter of fact, the standard 8 queens puzzle has 12 solutions (there are 92, actually, but the others are just reflections/rotations of the 12 fundamental ones)...

But the "10+9" puzzle only has three unique solutions that aren't reflections/rotations. I know two of them because they're very similar to each other, but I have no idea what the third one is.

Jutomi · Post by **Jutomi** » Tue Jan 14, 2014 10:15 pm

Well, having them like this...

O O O O O O O O
B W B W B W B W
O O O O O O O O
W B W B W B W B
O O O O O O O O
B W B W B W B W
O O O O O O O O
W B W B W B W B

... would surely be a 16+16 solution, right?

Though, having only a 10+9 solution's really mind-boggling for me.

Wow, do I wish I can find my chess board.

Muzozavr · Post by **Muzozavr** » Tue Jan 14, 2014 10:48 pm

You're misunderstanding the puzzle, trying to achieve the exact opposite outcome.

(which means: white can attack white, black can attack black, BUT white cannot attack black)

Your white never attacks white, your black never attacks black, but your whites and blacks constanly attack each other.

Jutomi · Post by **Jutomi** » Wed Jan 15, 2014 6:03 am

Oh, here's the answer for my third previous puzzle.
A bit late.

Hello There = 4.2(5).10(5).10(5).25(5) 1.4.2(5).40(5).2(5)

The rule for that one was to switch the English values of the letters backwards, and then cut them in half.

Now, for a hint of this last one...
Try thinking of three numbers and spinning things.

samuelthx · Post by **samuelthx** » Wed Jan 15, 2014 1:49 pm

Muzozavr wrote: I specifically avoided google searching to solve the puzzle by myself.

So, using a website that allowed me to drag-and-drop pieces and then generate a diagram image without me having to save the screenshot manually...

It really does work!

Congratulations!

My solution is like this:

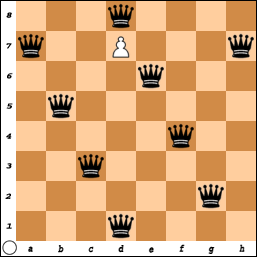
I took nearly half an hour to solve that puzzle!

As for your puzzle, it's really difficult! I might take days to solve this one...

Muzozavr · Post by **Muzozavr** » Sun Jan 19, 2014 11:37 pm

Has anyone managed to solve the puzzle I posted?

I assure you, it's perfectly solvable. The solution is rather weird, though.

Jutomi · Post by **Jutomi** » Mon Jan 20, 2014 1:18 am

Honestly, I have not even dared to touch it.

samuelthx · Post by **samuelthx** » Mon Jan 20, 2014 1:33 am

Muzozavr wrote:Has anyone managed to solve the puzzle I posted?

I assure you, it's perfectly solvable. The solution is rather weird, though.

Nope! Haven't got it yet. Don't post any hints first though (unless someone else asks for it)

Jutomi · Post by **Jutomi** » Mon Jan 27, 2014 2:53 am

This thing...

it seems to have gone dead without any body on.

Here's the answer to the previous question: 9913.

The second numbers are based off of the month, day, and year, and each of the first numbers are the amount of days past since 000(all so known as 0 in my puzzles).

Well, here's a much easier one that you may solve; one that might give you inspiration to figure out Muzozavr's.

I've tried his, but I can't find any sufficient chess boards.

I digress. Here's my new puzzle.

The colours in this sequence are:
Red, Black, Black, White, and Purple.

What would be the next colour in this sequence?

I'll give you a hint; It has to do with hands.

Edits 1 and 2: Changed two words.

Jutomi · Post by **Jutomi** » Tue Jan 28, 2014 8:22 pm

Err...

Mind if I have a link to that website?

samuelthx · Post by **samuelthx** » Wed Jan 29, 2014 12:28 pm

Jutomi wrote:Err...

Mind if I have a link to that website?

If you are talking about the link to the chess image generator, here you are!

http://www.chessvideos.tv/chess-diagram-generator.php

What could your puzzle possibly mean???

I haven't had time to sit down and legit solve your puzzle, Muzozavr...

Jutomi · Post by **Jutomi** » Wed Jan 29, 2014 6:08 pm

Want an other hint?

All so, thank you so much for the website!

Jutomi · Post by **Jutomi** » Thu Jan 30, 2014 5:31 am

Wait...

place 9 queens and 10 queens on a board...

Firstly, is this a larger board?

Secondly, does that mean only place these queens on a board?

Third, are there all ready other pieces on the board?

I am brain betwangled as to otherwise!

Muzozavr · Post by **Muzozavr** » Thu Jan 30, 2014 10:29 am

No larger boards.

Place 10 white queens and 9 black queens on an 8x8 (did you miss that?) board so that no two queens of opposite colors are attacking each other.

Note that I said opposite colors. You can happily place two (or more!) white queens NEXT to each other, they won't bite, it's fine. Same with black queens. White and black should not attack each other.

There's an obvious 8x8 solution (that can even be turned into 8x9 rather easily) but it's a dead end... the 10x9 solution is COMPLETELY different!

Also, no other pieces.

Jutomi · Post by **Jutomi** » Thu Jan 30, 2014 4:39 pm

I did miss that...

I think I am going crazy trying to figure this out.

Yes, I did think of putting queens behind other queens... and, even occasionally behind even more queens behind yet an other set of queens...

but, I just can't figure it out.

I did, however, find a solution to an 8+9 and a 7+12.

I guess I'll keep trying.

Muzozavr · Post by **Muzozavr** » Thu Jan 30, 2014 4:51 pm

8+9

It's the obvious one, right?

7+12

Wait... that's actually interesting...

Jutomi · Post by **Jutomi** » Thu Jan 30, 2014 5:10 pm

There's an obvious one...?