The Wonderland Board

Hi there,

This is a type of math puzzle that I dreamt up.

(Later on I discovered that it was already discovered by others on the web, but I don't think that they also thought of the 2-D version. )

It's called "Maximum non adjacent subsequence sum".

Given an array A[..], filled with numbers *(that I chose),
your mission is to find the maximum sum of a SUBSET of array A[..]
with the constraint that no 2 numbers are adjacent to each other.
That is, - the SUM that is MAXIMUM wins and is the correct answer.

PUZZLE 1: -- Array A[..]


PUZZLE 2: -- Array B[..]


For puzzle 2, do the same thing.
Both arrays have only 16 numbers each.

Hints:
In puzzle 1, you may add the first "5" and "9" together (=14),
but you may not add that "5" to "8" since "5" and "8" are adjacent.
You may skip and choose any numbers that you wish as long as
they are not neighbors. MAXIMUM SUM wins.

Let's see how many get the correct answers for both puzzles.

There is even a slim possibility that one array will have 2 equal answers,
= a tie, but it's not likely, the odds are against it.

**************************************************

Try to solve the 2-Dimensional version:

It is a 10x6 arrray, the same rules apply,
extended UP-DOWN as well as LEFT-RIGHT.
No adjacent numbers may be summed together,
that is:

A number may not be summed with the one to its adjacent LEFT or
adjacent RIGHT.
A number may not be summed with it's immediate UP or DOWN.
The MAXIMUM SUM wins.

Any numbers chosen will have an effect on the
availability of others.

For example, in the first line, if you chose "41" then you will
not be able to choose "85" in the lower line because they are adjacent.

PUZZLE 3: -- Array C[..][..]


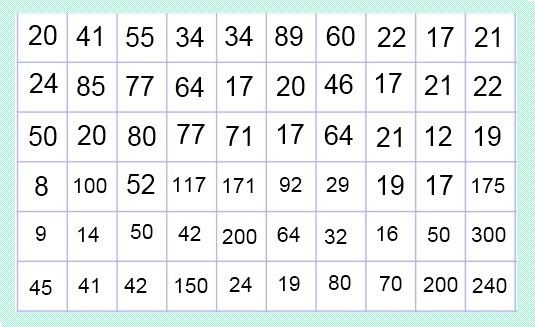
This is so hard that you may have to design a computer program to solve it.

O.K. then, it looks like no one was able to solve the 1st two puzzles,
( Puzzles 1 & 2 );
I created the following Blitz3D program to solve Puzzles 1 & 2:

Enjoy.

The heart of the recursive function is

Return max( MaxSum(N-1), A[N]+MaxSum(N-2) ),

where N is chosen to be the last index into the array A[].
In this case, the last index is A[15].

And the answers to the Puzzlers 1 & 2 are:

Max non-adj sum for {puzzle 1} = 48
Max non-adj sum for {puzzle 2} = 623

Of course, there are two obvious drawbacks with the current code

A: It does not list which actual numbers were summed up, and
B: It does not take into account that there may be two or
more different sequences that add up to the same sum (= a tie).

When I get back, I'll post an improved version which details all solutions.

I also have to figure out how to solve Puzzle 3, which is 2D.

There were other algorithms to solve the same thing, but my version
is the only one that I understand.
http://stackoverflow.com/questions/3733 ... n-an-array
http://nthrgeek.wordpress.com/2009/10/0 ... bsequence/

Blitz3D Demo:
http://www.blitzbasic.com/Products/_index_.php

Got 1 in 48, didn't try 2 and 3 yet...
EDIT: Got 2 in 623.

Solution for puzzle 1, left-to-right:

5+9+3+8+5+7+2+9=48

Solution for puzzle 2, left-to-right:

74+99+13+88+145+114+90=623

I actually got the first one before you even posted the max answer... it's just that 48 seemed ridiculously low to be the max answer. But it IS the max answer, as the program proves... so it was easy to find.

And puzzle 2 is still way easier than what I have to do for my science paper that I'm writing for school. And I have to write it faster than Sonic the Hedgehog runs. I thought I'd be able to talk with the teachers and postpone the project... but no, it's impossible.