Page 1 of 1
General Mathematics Discussion Thread
Posted: Fri Jul 06, 2012 8:08 pm
by tyteen4a03
Blast!10 wrote:This topic is to discuss anything and everything math related. Talk about conversion formulas, fun facts, proof, bitwise operators, algebra, and everything else.
On WolframAlpha, they have a very cool graph drawer that draws the graph according to the function given. I googled around and found this inequality, which draws a batman. The inequality is this:
Code: Select all
x^2/49+y^2/9-1<=0 and abs(x)>=4 and -(3 sqrt(33))/7<=y<=0 or abs(x)>=3 and y>=0 or -3<=y<=0 and -4<=x<=4 and (abs(x))/2+sqrt(1-(abs(abs(x)-2)-1)^2)-1/112 (3 sqrt(33)-7) x^2-y-3<=0 or y>=0 and 3/4<=abs(x)<=1 and -8 abs(x)-y+9>=0 or 1/2<=abs(x)<=3/4 and 3 abs(x)-y+3/4>=0 and y>=0 or abs(x)<=1/2 and y>=0 and 9/4-y>=0 or abs(x)>=1 and y>=0 and -(abs(x))/2-3/7 sqrt(10) sqrt(4-(abs(x)-1)^2)-y+(6 sqrt(10))/7+3/2>=0
SVG images are vector images defined with functions just like these. While very time-consuming to get it right, it does look beautiful at the end.
mathematics topic
Posted: Mon Jul 09, 2012 8:43 pm
by VirtLands
[ I deleted my previous post here, since it was not advancing ..]
Hi, yes it's an addicting topic, here are related links>
Wolfram Alpha:
http://www.wolframalpha.com/#
Wolfram Mathworld:
http://mathworld.wolfram.com/
Wolfram Math Online Integrator:
http://integrals.wolfram.com/index.jsp
Some of my Wolfram favorites:
_________________________________________________________
600-cell : hypericosahedron
http://en.wikipedia.org/wiki/600-cell
http://mathworld.wolfram.com/600-Cell.html
http://www.wolframalpha.com/input/?i=600-cell
120-cell : hecatonicosachoron
http://mathworld.wolfram.com/120-Cell.html
http://www.wolframalpha.com/input/?i=120+cell
_________________________________________________________
11-cell :
http://en.wikipedia.org/wiki/11-cell
16-cell : also known as hyperoctahedron or hexadecachoron
24-cell : also known as hyperdiamond or icositetrachoron
http://mathworld.wolfram.com/24-Cell.html
http://en.wikipedia.org/wiki/24-cell
_________________________________________________________
57-cell :
There are 57 vertices and each vertex connects to 6 others; I haven't
proved this to myself yet, so I'll take their word for it.
higher-resolution view at this link:
http://upload.wikimedia.org/wikipedia/c ... gs.svg.png
__________________________________________________________________________________________
Uniform polychorons: http://en.wikipedia.org/wiki/Uniform_po ... _H4_family
A stereographic preview of the 600-Cell:
Note: each vertex connects to 12 other vertexes.
Schläfli symbol {3,3,5}
It contains 1200 triangular faces, 720 edges, and 120 vertices. The edges form 72 flat regular decagons.
Each vertex of the 600-cell is a vertex of six such decagons.
http://en.wikipedia.org/wiki/File:Stere ... 00cell.png

Posted: Mon Jul 09, 2012 8:49 pm
by llarson
I LOOOOVE geometry so I guess I'll post about my favorite shape. Introducing: THE ICOSAGON
In other words: It's a 20 sided shape. Looks almost like a circle somewhat. I looked it up on wikipedia one time and it almost looked exaclty like a circle. BTW Virtlands is there an 100-sided shape?

Posted: Mon Jul 09, 2012 9:18 pm
by StinkerSquad01
There is a shape for any number of sides. 100 sided shape is 100-gon or Hectagon.
regular polyhedra, polygons, & polychorons
Posted: Mon Jul 09, 2012 9:28 pm
by VirtLands
llarson wrote:I LOOOOVE geometry so I guess I'll post about my favorite shape. Introducing: THE ICOSAGON
The IcosaGon: a 2-dimensional regular flat 20-sided shape:
http://mathworld.wolfram.com/Icosagon.html
Given a unit side length of u=1, you can accurately calculate the
inradius, circumradius, of an Icosagon as follows:
r = u * ½(1 + √5 + √(5 + 2√5)) : (inradius)
R = u * √(3 + √5 + ½√(50 + 22√5)) : (circumradius)
A = u² * 10(1 + √5 + √(5 + 2√5)) : (Area)
Posted: Mon Jul 09, 2012 9:29 pm
by llarson
WOW!

THANKS A LOT!!!!!!!!



Now where did that like button run off to?
defined irrationals in trigonometry
Posted: Mon Jul 09, 2012 11:16 pm
by VirtLands
In Trigonometry, ...
Some of the irrational SIN and COS values are precisely defined,
and some are NOT:
For Examples:
NOT perfectly defined : cos(10°) ≈ 0.9848077530
NOT perfectly defined : cos(11°) ≈ 0.9816271834
IS perfectly defined : COS(15°) = ¼(√6+√2)
IS perfectly defined : COS(18.75°) = ¼√ (8+2√(8+2(√6-√2)))
IS perfectly defined : SIN(45°) = √(0.5) ≈ 0.7071067811
Unbelievable as it is, here are two more unusual trig cases that ARE precisely defined:
cos( 360/17° ) = [-1 + √17 + √(34-2√17) + 2√(17 +3√17 -√(34-2√17) -2√(34+2√17) )]/16
sin( 20° ) = 2 * 2^(⅓) * (³√(i-√3) -³√(i+√3)) 
(where i=√-1, PI = 3.141592653589.., and ³√ may represent the third root of a complex number)
You can find a few more examples like this on these links:
Trigonometry Angles--Pi/5 : http://mathworld.wolfram.com/TrigonometryAnglesPi5.html
Trigonometry Angles--Pi/7 : http://mathworld.wolfram.com/TrigonometryAnglesPi7.html
Trigonometry Angles--Pi/9 : http://mathworld.wolfram.com/TrigonometryAnglesPi9.html
Trigonometry Angles--Pi/11 : http://mathworld.wolfram.com/Trigonomet ... sPi11.html
Trigonometry Angles--Pi/13 : http://mathworld.wolfram.com/Trigonomet ... sPi13.html
Trigonometry Angles--Pi/15 : http://mathworld.wolfram.com/Trigonomet ... sPi15.html
Trigonometry Angles--Pi/17 : http://mathworld.wolfram.com/Trigonomet ... sPi17.html
Trigonometry Angles--Pi/23 : http://mathworld.wolfram.com/Trigonomet ... sPi23.html
Trigonometry Angles : http://mathworld.wolfram.com/TrigonometryAngles.html
Okay, so maybe since sin(20°) is defined, then also sin(10°)
can also be perfectly defined using half-angle formulas.
There is more on this, but it's over my head right now.
Posted: Tue Jul 10, 2012 6:27 am
by tyteen4a03
sin/cos/tan(30, 45, 60, 90) are also precisely defined, and are more common.
The ³√ can also be represented with a power to 1/3.
Posted: Sun Aug 05, 2012 2:02 pm
by dlcs18
I figured out a formula which calculates the width/height of a rectangle if you have the area and the horizontal-to-vertical ratio.
(sqrt(a)*sqrt(b))/sqrt(c)
where:
a = the area of the rectangle
The values of b and c depend on if you want the width or the height of the region. If you want width:
b = the horizontal part of the ratio
c = the vertical part of the ratio
If you want height:
b = the vertical part of the ratio
c = the horizontal part of the ratio
For example, on a screen, a region of 640*480 pixels has the total pixel amount of 307200, and a ratio of 4:3
So if we insert these into the formula:
(sqrt(307200)*sqrt(4))/sqrt(3)
it will give us 640, which is the width of the region.
or to calculate the height, switch the 4 and 3 around:
(sqrt(307200)*sqrt(3))/sqrt(4)
which will give you 480, which is the height of the region.
Finding W,H, given Area and ratio
Posted: Mon Aug 06, 2012 6:54 pm
by VirtLands
Hello dlcs18, my hat's off to you.: Here's my version of the same events:
A = Area : r = ratio : h = height : w = width
( r=4/3 , A = 307200 )
h * (⁴/₃ h = 307200
h² * (⁴/₃) = 307200
h² = 307200 * (¾)
h² = 230400
h = 480
w = 480 * ⁴/₃ = 640
________________________________________________________
or, creating the algorithm, where height (h) = 'the shorter side', and r= w/h
A = h²*r
H = √( A/r ), W = H*r
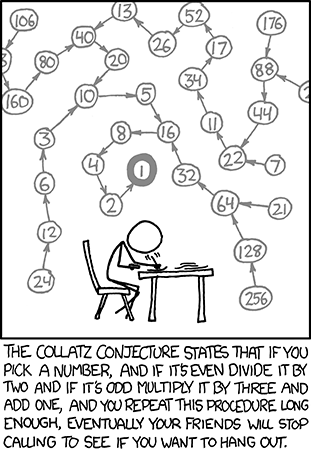
collatz_conjecture
Posted: Fri Dec 21, 2012 1:27 am
by VirtLands
--
-----

[
Doing stuff the hard way.. ]
--

-----

--
--

--

--
-----

--

--

--
 [ All of the above comix were taken from:
[ All of the above comix were taken from:
http://xkcd.com/about/
http://xkcd.com/archive/ ] 
-------------------------------------------------------------------------------------
Posted: Fri Dec 21, 2012 4:14 am
by L'Carpetron Dookmarriot 3
Posted: Fri Dec 21, 2012 4:26 am
by llarson
Solution wrote:Because the goat can't be alone with the cabbage  .
.
Posted: Fri Dec 21, 2012 4:38 am
by L'Carpetron Dookmarriot 3
There is supposed to be a solution where you bring all of them over, (even the wolf) but he tells us to just ignore the wolf because well, why would you have a wolf?
Posted: Fri Dec 21, 2012 5:04 am
by Sammy_P
At this point, we need a topic for xkcd.


 -----
----- 
 -----
----- 


 -----
-----